Comments on Substack.

The advice

Most advice I read online doesn’t work for me. For example, Zvi Mowshowitz’s post on applying timeless decision theory to habit-forming seemed like a revelation, but didn’t quite stick.

I’m writing this post about some advice I read on the Internet that has worked. This doesn’t necessarily mean it will work for you — from the house of Eliezer Yudkowsky:

You read nineteen different webpages advising you about personal improvement—productivity, dieting, saving money. And the writers all sound bright and enthusiastic about Their Method, they tell tales of how it worked for them and promise amazing results…

But most of the advice rings so false as to not even seem worth considering. […]

And then you read the twentieth piece of advice—or even more, you discover a twentieth method that wasn’t in any of the pages—and STARS ABOVE IT ACTUALLY WORKS THIS TIME.

At long, long last you have discovered the real way, the right way, the way that actually works. And when someone else gets into the sort of trouble you used to have—well, this time you know how to help them.

This is the fallacy of other-optimization.

Still, maybe Random Advice on the Internet working for one other person increases the odds that it’ll work for you? Here it is, from a Twitter exchange recently shared on LessWrong (emphasis mine):

Sarah Constantin: I really liked this example of an introspective process, in this case about the “life problem” of scheduling dates and later canceling them: https://malcolmocean.com/2021/08/internal-trust-dancing-date-scheduling-cancelling/

Eliezer Yudkowsky: See, if I’d noticed myself doing anything remotely like that, I’d go back, figure out which steps of thought were actually performing intrinsically necessary cognitive work, and then retrain myself to perform only those steps over the course of 30 seconds.

SC: if you have done anything REMOTELY like training yourself to do it in 30 seconds, then you are radically smarter/more able/etc than me and all the other people who do slower introspective practices.

SC: I don’t know whether to be impressed or to roll to disbelieve.

EY: I mean I suspect that this actually requires something like a fast perceptual view of minds as engines and thoughts as doing work and like actually draws on my mind design knowledge, but, even so, I ask: Do you constantly look back and ask “How could I have thought that faster?”

SC: No, I’ve never asked that.

EY: Okay, well, every time I’m surprised by reality I look back and think “What about my model and my way of thinking could I change that would have predicted that better, without predicting a bunch of other things worse?”

EY: When somebody at a MIRI workshop comes up with a math proof, I look over it and ask if there’s a way to simplify it. Usually, somebody else does beat me to inventing a proof first; but if my intuition says it was too complicated, I often am first to successfully simplify it.

EY: And every time I complete a chain of thought that took what my intuition says was a lot of time, I look back and review and ask myself “How could I have arrived at the same destination by a shorter route?”

EY: It’s not impossible that you have to be Eliezer Yudkowsky for this to actually work - I am never sure about that sort of thing, and have become even less so as time goes on - but if AI timelines were longer I’d tell somebody, like, try that for 30 years and see what happens.

EY: Man, now I’m remembering when I first started doing this consciously as a kid. I called it Shortening the Way, because a rogue rabbi had recently told me that “Kwisatz Haderach” was actually a reference to a Kabbalistic concept about teleportation, so that term was on my mind.

How the advice has worked for me

The fastest way to understand code

After getting some practice coding algorithms on LeetCode, I thought about which strategies worked best for debugging code that was failing some test cases.

Here’s one that doesn’t work: randomly adding prints. At least for me, an exploded view of the program state over time is only useful after I have formulated a hypothesis about what I expect to see. As Brian Kernighan and Rob Pike explain in The Practice of Programming:

As personal choice, we tend not to use debuggers beyond getting a stack trace or the value of a variable or two. One reason is that it is easy to get lost in details of complicated data structures and control flow; we find stepping through a program less productive than thinking harder and adding output statements and self-checking code at critical places. Clicking over statements takes longer than scanning the output of judiciously-placed displays. It takes less time to decide where to put print statements than to single-step to the critical section of code, even assuming we know where that is.

Another strategy that doesn’t work is staring at the code and guessing where the bug could be. Rather, the strategy that turned out to be consistently the fastest was stepping through the code by hand (I later learned this is called program tracing). (You don’t have to mentally simulate the program state, you’re allowed to scribble or draw it out — in fact, another thing I learned from “how could I have thought that faster?” introspection was to reach for paper more quickly. I have been vindicated by this interesting paper which finds that programmers can hold only about 7 variable/value pairs in their working memory during program tracing, and can swap them accidentally.)

One reason program tracing works is that LeetCode problems often have edge cases even if your overall logic is correct. For example, if you’re manipulating a linked list, something unexpected often happens while modifying the head. So, I was skeptical that program tracing could work in less contrived settings — or, if it did, that it would work better than staring at the code and trying to grok it.

As it turns out, it does.

A few days ago, I was trying to figure out what the update equations for gradient descent with momentum were doing:

\[\begin{align} v_t &= \gamma v_{t-1} + \eta \nabla_\theta J(\theta) \\ \theta &= \theta - v_t \end{align}\]

By this time, “how could I have thought this faster?” introspection had already bumped program tracing near the top of strategies to try. So, I started stepping through the code. And it soon became glaringly obvious that the gradient computed n steps ago would be diminished by the rate of decay raised to the power of n.

I think this is a non-trivial insight that would’ve been difficult to stumble upon by just staring at the update equations long enough. Even after reading the words [PDF] “The velocity is set to an exponentially decaying average of the negative gradient”, it can be difficult to internalize what an “exponentially decaying average” means. Program tracing helps make it truly part of you.

Reasoning from the smallest nontrivial case

Consider the pirate game, the first problem from the Green Book:

Five pirates looted a chest full of 100 gold coins. Being a bunch of democratic pirates, they agree on the following method to divide the loot:

The most senior pirate will propose a distribution of the coins. All pirates, including the most senior pirate, will then vote. If at least 50% of the pirates (3 pirates in this case) accept the proposal, the gold is divided as proposed. If not, the most senior pirate will be fed to shark and the process starts over with the next most senior pirate … The process is repeated until a plan is approved. You can assume that all pirates are perfectly rational: they want to stay alive first and to get as much gold as possible second. Finally, being blood-thirsty pirates, they want to have fewer pirates on the boat if given a choice between otherwise equal outcomes.

How will the gold coins be divided in the end?

The key is to reason from the simplest case, where there are just two pirates. The full solution is here. But what’s more important than knowing it is going “how could I have solved this faster (or, at all)?”, and noticing the general strategy. From the Green Book, the strategy is:

If the original problem is so complex that you cannot come up with an immediate solution, try to identify a simplified version of the problem and start with it. Usually you can start with the simplest sub-problem and gradually increase the complexity. You do not need to have a defined plan at the beginning. Just try to solve the simplest cases and analyze your reasoning. More often than not, you will find a pattern that will guide you through the whole problem.

Armed with this insight, you can tackle the sheep-eating tigers and the blue-eyed islanders problems. But can you do more than solve logic puzzles?

Yes. You can avoid proving that all horses are the same color.

Even more?

I don’t know about you, but the incantation that “linear classifiers are multi-dimensional hyperplanes cutting up space” broke my brain a little when I first heard it. I decided to understand the 2D case really well first, and it turned out to be simple to reason upwards from that.

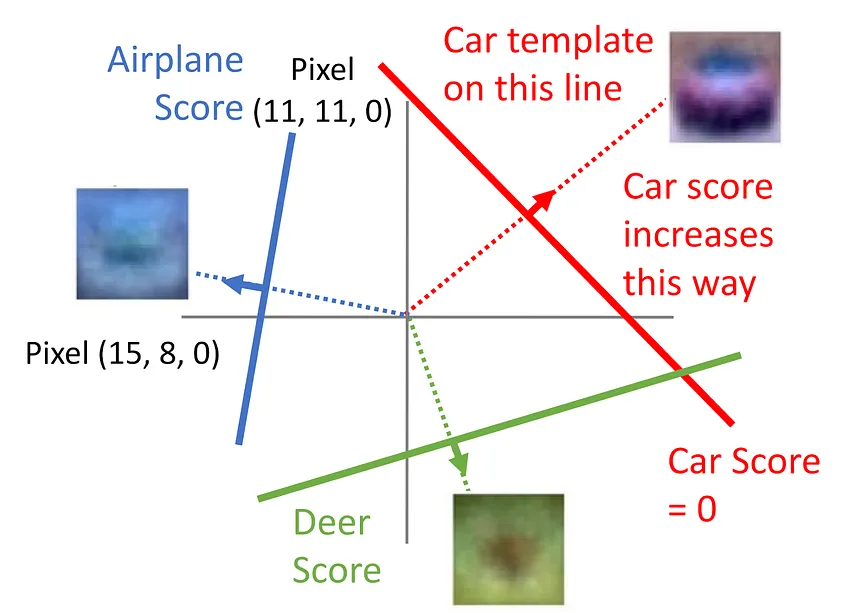The 2D view of linear classifiers. Via Justin Johnson’s (excellent) deep learning lectures at UMich.

Look up technical terms

Until not too long ago, I used to think that Jacobians are a special and difficult idea. It turned out that just reading the Wikipedia article on Jacobians is enough to understand how to work with them (if you know what a derivative is). This has happened to me several times: I’d heard the words “Markov chain” and “Lagrange multiplier” somewhere, and assumed they were exotic concepts. But they can be picked up in about fifteen minutes each (though Lagrange multipliers require knowing a little bit of multivariable calculus).

After this many iterations, “how could I have thought this faster?” should kick in. And it has. Before, my default behavior when I came across an unfamiliar term in a technical text was to skim ahead quickly and make sure the term wasn’t invoked too many times again. (This sounds like a bad idea, but works well surprisingly often. For example, even if your deep learning notes formalize things with the Jacobian, you can understand and even code up the backpropagation algorithm without it.)

Now, when I come across an unfamiliar term, I make it a point to quickly look it up. (I don’t ask a language model what it means. In my experience, LLMs work better for clarifying concepts than for introducing completely new ones.) After all, if the term is in a technical text I’m already reading, it cannot be that far above my level.


Hopefully, these examples show what “how could I have thought that faster?” looks like in practice (for one (1) individual). The next time something takes a while to click, maybe ask yourself which steps in your reasoning were the most fruitful, and keep those near the top of things to try on similar problems.